entropy
The entropy of a variable is a sort of average surprise.
This is the discrete case, a parallel exists for continuous events in the form of differential entropy.
\begin{equation}
H(X) = -\sum_{i = 1}^{n} p(x_i) \log{p(x_i)}
\end{equation}
When the log base is 2 (as it should always be), entropy is simply given in bits, as the number of bits needed to fully encode the event space. In general, this ideal bit sequence is given by huffman coding.
Note some properties of the idea of surprise, \(-\log{p(x_1)}\):
- rarer events (lower \(p\)) have a higher "surprise factor"
- so, if \(p(x)\) is 1, then we expect something to happen always, so there is no surprise.
- if two events are independent, the event of both happening at once should add in surprise.
Entropy is thus the expectation of surprise.
However, rarer events also happen less frequently, so they are "weighted" by their probability.
Some extra properties:
- Adding or removing an event with probability 0 does not affect entropy
- jensen inequality: \(H(X) \leq \log{n}\). In addition, this is achieved when the events are uniform (and so the only way to code the data is to enumerate) when the events are discrete.
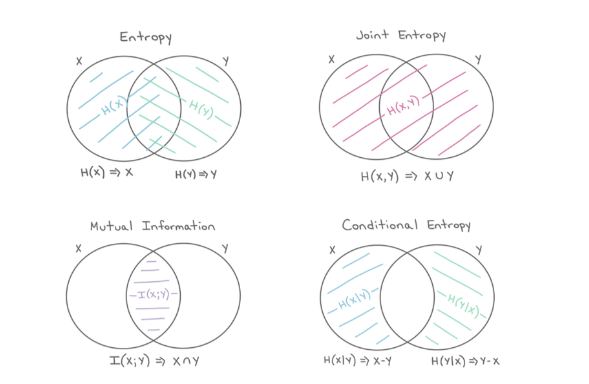
There exist other forms of multivariate entropy:
These forms are tighly interconnected, as shown in this diagram: